The area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, to a lesser extent, an investigation into the mathematical methods and notation of the past.
Before the modern age and the worldwide spread of knowledge, written examples of new mathematical developments have come to light only in a few locales. The most ancient mathematical texts available are Plimpton 322 (Babylonian mathematics c. 1900 BC), theRhind Mathematical Papyrus (Egyptian mathematics c. 2000-1800 BC) and the Moscow Mathematical Papyrus (Egyptian mathematics c. 1890 BC). All of these texts concern the so-called Pythagorean theorem, which seems to be the most ancient and widespread mathematical development after basic arithmetic and geometry.
The Greek and Hellenistic contribution greatly refined the methods (especially through the introduction of deductive reasoning and mathematical rigor in proofs) and expanded the subject matter of mathematics. The study of mathematics as a subject in its own right begins in the 6th century BC with the Pythagoreans, who coined the term "mathematics" from the ancient Greek μάθημα (mathema), meaning "subject of instruction".Chinese mathematics made early contributions, including a place value system.The Hindu-Arabic numeral system and the rules for the use of its operations, in use throughout the world today, likely evolved over the course of the first millennium AD in India and was transmitted to the west via Islamic mathematics.Islamic mathematics, in turn, developed and expanded the mathematics known to these civilizations.Many Greek and Arabic texts on mathematics were then translated into Latin, which led to further development of mathematics in medieval Europe.
From ancient times through the Middle Ages, bursts of mathematical creativity were often followed by centuries of stagnation. Beginning inRenaissance Italy in the 16th century, new mathematical developments, interacting with new scientific discoveries, were made at anincreasing pace that continues through the present day.
Modern mathematics
[edit]19th century
Throughout the 19th century mathematics became increasingly abstract. In the 19th century lived Carl Friedrich Gauss (1777–1855). Leaving aside his many contributions to science, in pure mathematics he did revolutionary work on functions ofcomplex variables, in geometry, and on the convergence of series. He gave the first satisfactory proofs of the fundamental theorem of algebraand of the quadratic reciprocity law.
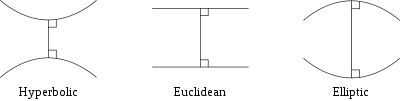
This century saw the development of the two forms of non-Euclidean geometry, where the parallel postulate of Euclidean geometry no longer holds. The Russian mathematician Nikolai Ivanovich Lobachevsky and his rival, the Hungarian mathematicianJános Bolyai, independently defined and studied hyperbolic geometry, where uniqueness of parallels no longer holds. In this geometry the sum of angles in a triangle add up to less than 180°.Elliptic geometry was developed later in the 19th century by the German mathematician Bernhard Riemann; here no parallel can be found and the angles in a triangle add up to more than 180°. Riemann also developed Riemannian geometry, which unifies and vastly generalizes the three types of geometry, and he defined the concept of a manifold, which generalize the ideas of curves and surfaces.
The 19th century saw the beginning of a great deal of abstract algebra. Hermann Grassmann in Germany gave a first version of vector spaces,William Rowan Hamilton in Ireland developed noncommutative algebra. The British mathematician George Boole devised an algebra that soon evolved into what is now called Boolean algebra, in which the only numbers were 0 and 1. Boolean algebra is the starting point ofmathematical logic and has important applications in computer science.
Augustin-Louis Cauchy, Bernhard Riemann, and Karl Weierstrass reformulated the calculus in a more rigorous fashion.
Also, for the first time, the limits of mathematics were explored. Niels Henrik Abel, a Norwegian, and Évariste Galois, a Frenchman, proved that there is no general algebraic method for solving polynomial equations of degree greater than four (Abel–Ruffini theorem). Other 19th century mathematicians utilized this in their proofs that straightedge and compass alone are not sufficient to trisect an arbitrary angle, to construct the side of a cube twice the volume of a given cube, nor to construct a square equal in area to a given circle. Mathematicians had vainly attempted to solve all of these problems since the time of the ancient Greeks. On the other hand, the limitation of three dimensions in geometry was surpassed in the 19th century through considerations of parameter space and hypercomplex numbers.
Abel and Galois's investigations into the solutions of various polynomial equations laid the groundwork for further developments of group theory, and the associated fields of abstract algebra. In the 20th century physicists and other scientists have seen group theory as the ideal way to study symmetry.
In the later 19th century, Georg Cantor established the first foundations of set theory, which enabled the rigorous treatment of the notion of infinity and has become the common language of nearly all mathematics. Cantor's set theory, and the rise of mathematical logic in the hands of Peano, L. E. J. Brouwer, David Hilbert, Bertrand Russell, and A.N. Whitehead, initiated a long running debate on the foundations of mathematics.
The 19th century saw the founding of a number of national mathematical societies: the London Mathematical Society in 1865, the Société Mathématique de France in 1872, the Circolo Mathematico di Palermo in 1884, the Edinburgh Mathematical Society in 1883, and theAmerican Mathematical Society in 1888. The first international, special-interest society, the Quaternion Society, was formed in 1899, in the context of a vector controversy.
[edit]20th century
The 20th century saw mathematics become a major profession. Every year, thousands of new Ph.D.s in mathematics are awarded, and jobs are available in both teaching and industry.
In a 1900 speech to the International Congress of Mathematicians, David Hilbert set out a list of 23 unsolved problems in mathematics. These problems, spanning many areas of mathematics, formed a central focus for much of 20th century mathematics. Today, 10 have been solved, 7 are partially solved, and 2 are still open. The remaining 4 are too loosely formulated to be stated as solved or not.
Notable historical conjectures were finally proved. In 1976, Wolfgang Haken and Kenneth Appelused a computer to prove the four color theorem. Andrew Wiles, building on the work of others, proved Fermat's Last Theorem in 1995. Paul Cohen and Kurt Gödel proved that the continuum hypothesis is independent of (could neither be proved nor disproved from) the standard axioms of set theory. In 1998 Thomas Callister Hales proved the Kepler conjecture.
Mathematical collaborations of unprecedented size and scope took place. An example is theclassification of finite simple groups (also called the "enormous theorem"), whose proof between 1955 and 1983 required 500-odd journal articles by about 100 authors, and filling tens of thousands of pages. A group of French mathematicians, including Jean Dieudonné and André Weil, publishing under the pseudonym "Nicolas Bourbaki", attempted to exposit all of known mathematics as a coherent rigorous whole. The resulting several dozen volumes has had a controversial influence on mathematical education.[113]
Differential geometry came into its own when Einstein used it in general relativity. Entire new areas of mathematics such as mathematical logic, topology, and John von Neumann's game theorychanged the kinds of questions that could be answered by mathematical methods. All kinds ofstructures were abstracted using axioms and given names like metric spaces, topological spacesetc. As mathematicians do, the concept of an abstract structure was itself abstracted and led tocategory theory. Grothendieck and Serre recast algebraic geometry using sheaf theory. Large advances were made in the qualitative study of dynamical systems that Poincaré had begun in the 1890s. Measure theory was developed in the late 19th and early 20th centuries. Applications of measures include the Lebesgue integral, Kolmogorov's axiomatisation of probability theory, andergodic theory. Knot theory greatly expanded. Quantum mechanics led to the development offunctional analysis. Other new areas include , Laurent Schwarz's distribution theory, fixed point theory, singularity theory and René Thom's catastrophe theory, model theory, and Mandelbrot'sfractals. Lie theory with its Lie groups and Lie algebras became one of the major areas of study.
The development and continual improvement of computers, at first mechanical analog machines and then digital electronic machines, allowed industry to deal with larger and larger amounts of data to facilitate mass production and distribution and communication, and new areas of mathematics were developed to deal with this: Alan Turing's computability theory; complexity theory; Claude Shannon's information theory; signal processing; data analysis; optimization and other areas of operations research. In the preceding centuries much mathematical focus was on calculus and continuous functions, but the rise of computing and communication networks led to an increasing importance of discrete concepts and the expansion of combinatoricsincluding graph theory. The speed and data processing abilities of computers also enabled the handling of mathematical problems that were too time-consuming to deal with by pencil and paper calculations, leading to areas such as numerical analysis and symbolic computation. Some of the most important methods and algorithms discovered in the 20th century are: the simplex algorithm, the Fast Fourier Transformand the Kalman filter.
At the same time, deep insights were made about the limitations to mathematics. In 1929 and 1930, it was proved the truth or falsity of all statements formulated about the natural numbers plus one of addition and multiplication, was decidable, i.e. could be determined by some algorithm. In 1931, Kurt Gödel found that this was not the case for the natural numbers plus both addition and multiplication; this system, known as Peano arithmetic, was in fact incompletable. (Peano arithmetic is adequate for a good deal of number theory, including the notion ofprime number.) A consequence of Gödel's two incompleteness theorems is that in any mathematical system that includes Peano arithmetic (including all of analysis and geometry), truth necessarily outruns proof, i.e. there are true statements that cannot be proved within the system. Hence mathematics cannot be reduced to mathematical logic, and David Hilbert's dream of making all of mathematics complete and consistent needed to be reformulated.
One of the more colorful figures in 20th century mathematics was Srinivasa Aiyangar Ramanujan(1887–1920), an Indian autodidact who conjectured or proved over 3000 theorems, including properties of highly composite numbers, the partition function and its asymptotics, and mock theta functions. He also made major investigations in the areas of gamma functions, modular forms,divergent series, hypergeometric series and prime number theory.
Paul Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. Mathematicians have a game equivalent to the Kevin Bacon Game, which leads to the Erdős number of a mathematician. This describes the "collaborative distance" between a person and Paul Erdős, as measured by joint authorship of mathematical papers.
As in most areas of study, the explosion of knowledge in the scientific age has led to specialization: by the end of the century there were hundreds of specialized areas in mathematics and the Mathematics Subject Classification was dozens of pages long.[114] More and moremathematical journals were published and, by the end of the century, the development of the world wide web led to online publishing.
21st Century
In 2000, the Clay Mathematics Institute announced the seven Millennium Prize Problems, and in 2003 the Poincaré conjecture was solved byGrigori Perelman (who declined to accept any awards).
Most mathematical journals now have online versions as well as print versions, and many online-only journals are launched. There is an increasing drive towards open access publishing, first popularized by the arXiv.



No comments:
Post a Comment